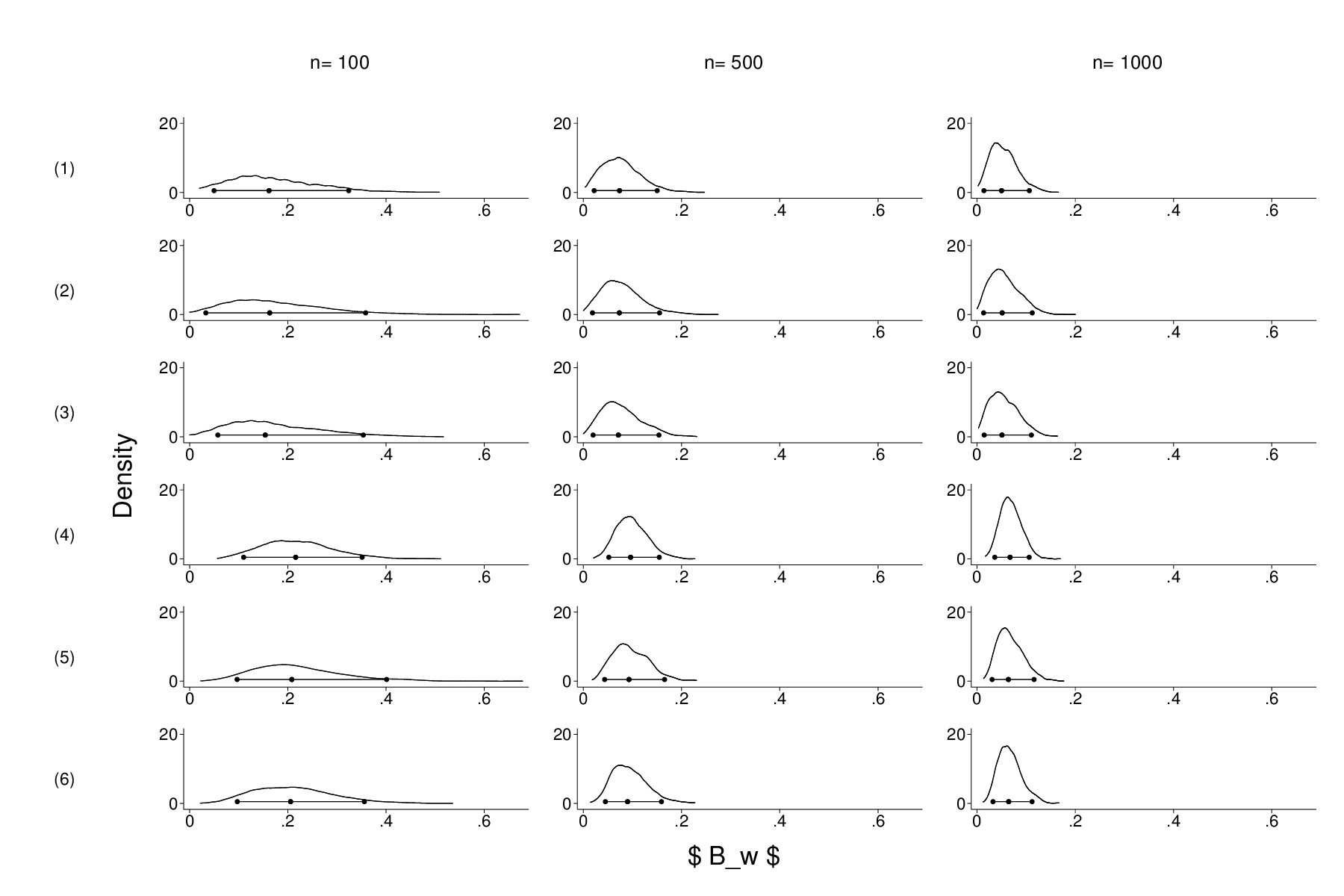
Data: How many people are shot dead or otherwise killed in OECD countries?
As a follow-up to my recent post on the relationship between gun ownership and gun homicide in OECD countries, I have rolled my dataset (compiled from information published by gunpolicy.org) and my analysis script into a neat Stata package. If you want to recreate the tables and graphs, or otherwise want to play with the…