1 Introduction
During the last 15 years, the (aggregate) analysis of electoral turnout in liberal democracies has become a minor industry. A recent survey of the relevant literature (Geys, 2006) lists not fewer than 83 empirical studies that relate turnout to a plethora of institutional, political and social factors. Amongst these, population size, the closeness of the respective contest, and (a rather less surprising finding) compulsory voting emerge as the most important independent variables. Michael Lister’s (2007) recent article in this journal is a valuable addition to this discussion, because by focusing on social inequality, he draws our attention to a whole host of societal factors that have by and large been neglected so far. Moreover, Lister’s contribution is one of the few studies that analyses turnout over time and in a cross-national perspective, whereas the majority of the analyses looks at subnational units, often in a cross-sectional perspective.
There are, however, a number of methodological and substantive issues with Lister’s analysis that call the validity of his findings into question: First, Lister’s account of causal relationships is highly problematic, second, the methodology is not appropriate given the low and unequal number of elections per year, third, most variables in the model are constant or near-constant within countries, and forth, even if there is a statistically significant relationship between inequality and turnout, it is trivial. In what follows, I will address these points in turn.
2 Is there an effect of inequality on turnout?
2.1 Causality
Macro level welfare state institutions 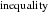 
|
Lister’s central argument is that the institutions of the welfare state shape citizens’ expectations (or norms) and thereby their political behaviour (Lister, 2007, 25). More specifically, he argues that welfare state institutions which are based on universalist principles provide ‘more support for norms of solidarity’ (Lister, 2007, 25). These norms encourage electoral participation both directly and indirectly. Means-tested welfare programs, on the other hand, have opposite effects (Lister, 2007, 25). Building on Coleman’s (1994, 7) framework for sociological explanation, his argument can be reconstructed in a slightly simplified way by employing three causal statements (see Figure 1):
- Features of the welfare state (a macro-level variable) affect internalised norms and expectations, i.e. individual attitudes.
- These individual attitudes have an impact on an individual’s decision to participate in a national election
- These individual decisions constitute turnout, another macro-level variable
Amongst these, only the third statement is unproblematic since it involves a purely mechanical aggregation (given that in liberal democracies, people are normally not prevented from voting in any systematic way). Statements (a) and (b) on the other hand are rather bold claims about the consequences and antecedents of individual variables which can never be proven right or wrong on the basis of macro-data. Ever since Robinson (1950) published his famous paper on ecological correlation, social scientists have struggled with the problem of ecological fallacies, i.e. the impossibility of deriving valid conclusions about individual behaviour from the aggregate measures.
Even the most advanced statistical techniques in the field that aim at making probabilistic statements about the likely strength of relationships between micro-level variables (say race and voting in a two-party competition, see King 1997) rely on information about the distribution of micro-level variables on the macro-level. In the absence of such information on the distribution of individual norms and expectations, nothing can be said about the validity of statements (a) and (b). Moreover, the analysis presented in Lister relies on another unobserved relationship, namely the causal connection between the institutions of the welfare state and inequality between households (d). While the nature of the welfare state’s institutions at any given point t (‘universalistic’ vs. ‘liberal’ or ‘minimal’ arrangements) will arguably have a substantial effect on inequality between households at t, it will hardly completely determine the current level of inequality. Rather, a whole host of other factors including the global and the national economy, the system and level of taxation, the previous level of inequality at points t – 1,t – 2,… as well as the previous nature of welfare state institutions and all sorts of unintended consequences and side-effects of previous policy will affect the current level of inequality, making this a rather crude measure of welfare state arrangements. Finally, over and above serving as an indicator for welfare state arrangements, inequality in itself can easily have a positive or a negative impact on one’s internalised norms and attitudes, thereby either masking or exaggerating the importance of causal effects that work along path (a). On the one hand, very low and falling levels of inequality (which are presumably associated with very high tax rates) could encourage the parties of the centre and the right to mobilise the middle classes, which would ceteris paribus lead to an increase in turnout. On the other hand, a high level of inequality would provide the working class with an incentive to vote in order to achieve a more comprehensive welfare state — this is the logic of the ‘democratic class struggle’ (Anderson and Davidson, 1943).1
To summarise, while Lister’s article builds on a complex framework involving three aggregate and two micro-level variables, claims about three causal relationships which are crucial for the argument and a fourth which can potentially distort the results are not and cannot be backed by data. Therefore, any conclusions from the analysis are confined to claims about the relationship between inequality and turnout on the aggregate level (i.e. ‘polities which face a high level of inequality will ceteris paribus experience a high/lower turnout than those with a more egalitarian distribution of resources’).
2.2 Data and Modelling
2.2.1 Data
The analysis presented by Lister relies chiefly on a single source which is in the public domain: the ‘Comparative Welfare States Data Set’ (Huber et al., 2004) that compiles information for 18 countries from a variety of sources, covering the time-span from 1960-2000. This data set provides information on turnout (VTURN, drawn from Mackie and Rose 1982 and the reports in the European Journal of Political Research) as well as on a number of control variables such as a (chain) index of GDP per capita (RGDPC), the strength of bicameralism (STRBIC), the presence and strength of federalism (FED),2 the proportionality of the electoral system (SINGMEMD), and whether the respective country has a presidential system (PRES). These are merged with information on the focal independent variable income inequality (INEQ), which comes from the University of Texas Inequality Project (2004), and a report on compulsory voting (COMPVOTE) which was compiled by IDEA (Gratschew, 2001).
While Lister dismisses welfare state spending data very quickly, comparing income inequality across time and countries is full of pitfalls (Atkinson and Brandolini, 2000). There is no discussion of the quality and particular features of the data from the University of Texas Inequality Project whatsoever, and alternative data sources such as the Luxembourg Income Study (Atkinson, 2004) that might well be better suited for the research problem at hand are not even considered.
More generally relying on data sets in the public domain has clear advantages in terms of availability and replication, yet it imposes equally clear restrictions on the selection of observations and the time-frame (1963-93), which are not addressed in the text. This notwithstanding, it would have been helpful to discuss the rationale for not including Norway and New Zealand in the analysis, although these countries are covered by the sources, since the inclusion/exclusion of a single country can substantially affect the results of the regression model (see section 2.2.3 below).3
|
To replicate Lister’s findings as closely as possible, a data set (available from hdl:1902.1/10558 UNF:3:2UNq+CMPvmjb7Aat9NvpKw==) was constructed in the following way: from the Comparative Welfare States Data Set, the 15 countries under study were selected. For those, all election years between 1963 and 1993 were retained (averaging over the 1974/1982 elections for the UK and Ireland), resulting in 136 observations with non-missing values for turnout, federalism, presidentialism, bicameralism, and GDP per capita.
Best efforts notwithstanding, it proved impossible to reproduce Lister’s findings exactly, although the differences are fairly small.4 More troubling is the fact that at first glance, the coefficients reported by Lister do not seem to sum up. If one plugs in the mean values5 for all the independent variables, the expected turnout is a staggering 161 per cent (see Table 1). However, the magnitude of the coefficients and the constant reveals that the author has converted turnout6 from its original percentage scale to a relative frequency scale and then applied a logit transformation to the new variable to account for the fact that the dependent variable is bound to the interval [0;100].7
Accordingly, lagged turnout (VTURNLAG) was constructed by taking the turnout from the previous election for all election years as outlined in footnote 4 while LOGITVTURN was constructed as ln
2.2.2 Inappropriate Methodology
The data constitute a Time-Series-Cross-Sectional (TSCS) or panel arrangement: (very short) time series from n = 15 countries are pooled and analysed jointly. In political science, this design became extremely popular after Beck and Katz (1995, 1996) suggested that the familiar Ordinary Least Squares (OLS) estimator can be applied to this specific data structure as long as the standard errors are ‘panel corrected’ (PCSE) to account for the dependencies amongst observations.
Following Beck and Katz (1995, 636), a generic TSCS model can be written as
| (1) |
where y is the dependent variable, x is a vector of independent variables (including the constant), ε is a random error term, and observations are indexed by unit/country (i) and time (t). With TSCS data, the standard assumptions of regression analysis are likely to be violated as one would expect the ε to be ‘non-spherical’ that is, contemporaneously correlated, heteroscedastic, and serially correlated (Beck and Katz, 1995, 636), rendering ‘raw’ standard errors invalid and thereby giving rise to confidence intervals that are too narrow and significance tests that are too generous.9
(Positive) contemporaneous correlation, which is a consequence of unobserved factors increasing or decreasing turnout in several countries at the same time, cannot be ruled out completely but is unlike to pose huge problems for the analysis since the unit of observation is the national election.10 On the other hand, heteroscedasticity (the variance of ε is greater in country i than in country i + 1) is very likely to occur in the case of turnout: in countries where voting is compulsory, the variance of ε is bound to be smaller than in other polities.
Finally, the presence of (positive) serial correlation (the impact of some unobserved factor that affects turnout in country i at time t will still be felt at t + 1 and possibly t + 2,t + 3,…) can be taken for granted. Like most analysts of TSCS data, Lister follows the suggestions by Beck and Katz and accounts for this problem by including the lagged dependent variable (LDV).
This leads, however, to an intricate complication. The length of the election period varies both over time and across countries, e.g. it is fixed at four years in the US, comes empirically very close to the same value in the UK and in Italy, and varies between one year and five years in Canada (where there is a moderate upward trend in the duration of the election period). As a consequence, the autocorrelation of ε will also vary across countries and over time. The approach chosen by Lister does not deal with this, and even if it did, estimating a multitude of autocorrelations poses obvious problems, especially given the low N and T. While one could hope that the inclusion of the LDV somehow ameliorates the situation, exactly the same problems apply to the coefficient for the LDV which should again vary with the length of the election period. Therefore, any findings should be interpreted with extra caution.
* p<0.05, ** p<0.01, *** p<0.001.
|
Given the likely presence of heteroscedasticity and autocorrelation, applying the corrections outlined by Beck and Katz seems to be a sensible strategy at first glance. However, the approach by Beck and Katz was developed for balanced panels consisting of say 10 to 40 time periods (Beck and Katz 1995, 640-642; Beck 2007, 97). In the data set compiled for this analysis, T ≥ 10 in only six countries with a maximum of 13 in Denmark while the number of panel waves is just 7 to 9 in five other countries and extremely low (4 to 6) in four other countries. Under these conditions, PCSEs are not guaranteed to perform well (see Shor et al. 2007 for a review of the associated problems).
As a simple safeguard, a non-parametric bootstrapping procedure (Efron and Tibshirani, 1993) was applied, that is, 200 samples of n = 129 were drawn from the original data set (with replacement), and the analysis was repeated for each of these samples, thereby simulating the process that generated the data. Since each of these samples is slightly different from the others, the parameter estimates will vary, too. This variation generally provides a realistic approximation for the standard error in circumstances where the distributional assumptions might not hold. The results are shown in column 2 of Table 2. Compared with the first column, the t-values are substantially reduced, rendering all independent variables except compulsory voting and the LDV insignificant.
However, the unequal and rather low T suggests an alternative robustness check with an estimator that does not rely on the time-series nature of the data. Amongst the host of estimators available for panel data, Generalised Estimating Equation Models (GEE) have recently gained prominence in political science because they can accommodate complex structures for the correlation of ε and are fairly robust against misspecification (Zorn, 2001).11 As it turns out, this method yields almost identical point estimates, and again, compulsory voting and the LDV emerge as the only variables with statistically significant effects (column 3). The upshot is that the calculation of PCSE in Lister’s original analysis of the turnout data is not appropriate and leads him to overconfident conclusions.
2.2.3 Unit Effects and Lack of Variation over Time
But there are even more fundamental issues with this analysis of turnout and inequality. First, one must be sure that the units (countries) can be pooled, i.e. that (roughly) the same slope coefficient(s) prevail(s) in all countries. In the turnout data set, a rigorous check of this assumption that would involve the estimation of country-specific models is impossible because the institutional control variables are constant or almost constant within countries.12 Second, one must check for the presence of unit effects, i.e. for country-specific intercepts.13 If units are pooled and unit effects are not accounted for, massive bias can result. For instance, if some variable x has a moderately positive effect on y within two countries A and B, and the average value of x is higher in country B while the overall level of y is higher in country A, a coefficient with a negative sign might be estimated unless country-specific intercepts are included in the model.14 Unfortunately, it is not possible to test for unit effects since the institutional variables do not vary within countries and are therefore perfectly collinear with the country-specific intercepts. Moreover, there are non-trivial linear dependencies between the independent variables: federalism and bicameralism correlate at r = 0.41,15 the correlation between federalism and proportionality is -0.4816 and even inequality and proportionality correlate at -0.44.
|
To make things worse, the focal independent variable is ‘sluggish’ (Beck, 2001; Wilson and Butler, 2007; Plümper and Troeger, 2007), i.e. inequality varies a lot between countries but does not vary much within most countries (see Figure 2). While there are marked upward trends in Australia, Belgium, and the UK, and some apparently random variation in the Netherlands, inequality is largely stable elsewhere. Therefore, roughly 80 per cent of the total variation occurs between countries.
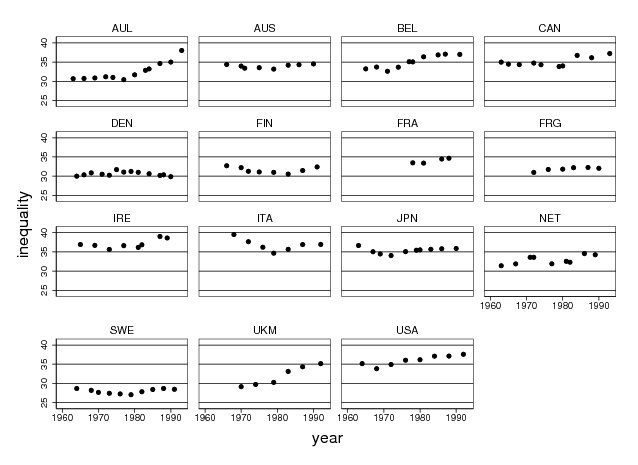
In a similar fashion, the variation of turnout within most countries is very moderate if compared to the variation between countries (see Figure 3). Turnout is consistently close to 100 per cent in Australia and Belgium (where compulsory voting is enforced) and still very high (i.e. above 80 per cent) in Austria, Denmark, Italy, and Sweden,17 whereas the figure for Japan hovers consistently around 70 per cent, and turnout in the US is permanently below or just above 60 per cent. Across the whole sample, only about 10 per cent of the total variation in turnout (or its transformation) occurs within countries while between-country differences account for the lion’s share of the variation.
|
There are other issues here. Although the inclusion of the LDV was championed by Beck and Katz, the LDV is likely to cause problems. Estimates will be biased even if the errors are uncorrelated, and inconsistent in the presence of correlation amongst the errors (Ostrom, 1990, 62-65).18 There is a whole host of alternative dynamic specifications (Wilson and Butler, 2007, 106), and, as Wilson and Butler demonstrate, these can give wildly different estimates in many cases.
Yet, the most fundamental problem of the analysis at hand is this: like many (if not most) other comparative data sets, the turnout data are plagued by collinearity and a lack of intra-unit variation and are therefore not very informative (Western and Jackman, 1994).19 With most of the variation in both the dependent and the independent variables occuring between countries, one can be quite sure that polity-level factors have an effect on turnout, but it is not possible to disentangle the relative effects of the various variables that are constant (like federalism), do not vary much (like inequality) or are constant but not included in the model (unit effects). There is something about the US that depresses turnout while there is something about Australia that drives turnout close to its theoretical maximum, but while registration procedures and compulsory voting are highly likely suspects, it is not possible to prove that these factors are decisive.
No methodology, however advanced, can overcome this basic lack of independent pieces of information. Given this fundamental problem, it is not surprising that the estimates for the effect of inequality (and the other independent variables) are rather unstable and depend on the inclusion/exclusion of certain observations. This can be most easily demonstrated by removing all observations from a given year or country from the sample. For instance, the coefficient for inequality is reduced from -0.024 to -0.018 if the four elections in 1971 are excluded. By contrast, the coefficient goes up to -0.028 if the four observations in 1970 are excluded. The impact of excluding a single country is even more dramatic: if Austria (eight observations), a country with average inequality but high turnout rates, is removed from the sample, the coefficient rises to -0.038. Excluding Sweden (ten observations), a country with low inequality and high turnout, reduces the estimate to -0.016. Even excluding single observations can have a discernible impact on the estimates: without the Australian general election of 1993, the estimate for the coefficient is -0.028, while excluding the Dutch general election of 1971 brings it down to -0.017. In other words, removing a single observation from the sample can result in a change of the estimate that is roughly equivalent to one standard error.
|
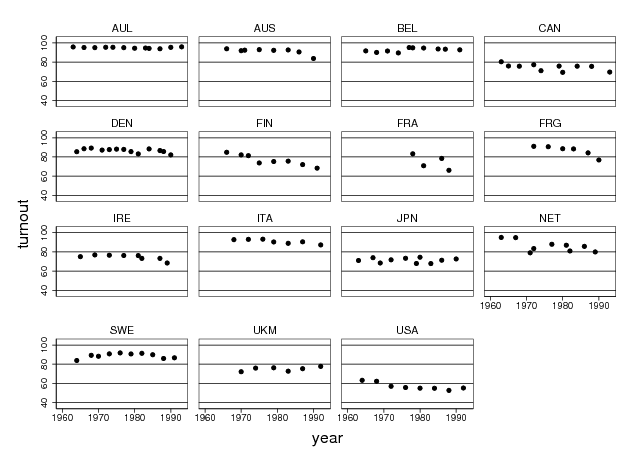
So is there anything at all that can be said about the relationship between inequality and turnout? The short answer turns out to be ‘no, not really’. One very basic approach is to ignore the institutional control variables as well as the potential impact of the GDP and to analyse the bivariate relationship on a per-country basis (see Fisher 2007 for a related bivariate analysis of turnout and the left vote).20 Figure 4 shows the respective scatter plots, with country-specific linear regression lines overlaid. This figure is quite revealing. Leaving aside the very low variation along both the x- and the y-axis in most countries, only five polities — Austria, France, West Germany, the Netherlands, and Sweden — display a clearly negative relationship between inequality and turnout, and even this statement requires qualification. Fitting any sort of trend to four data points (France) is obviously risky, and the variation of inequality is extremely low in Sweden, Austria, and West Germany. Moreover, the clear-cut negative trend in Austria and West Germany hinges on one outlying election respectively, which happens to be the rather unusual first election immediately after unification in Germany. This leaves the Netherlands as the only real example for the negative relationship between inequality and turnout. In all other countries, the relationship is weakly positive or close to nil.
PCSELOGITVTURN VTURN
* p<0.05, ** p<0.01, *** p<0.001.
|
To carry out a more formal test, one could run a final pooled regression of turnout on inequality and control for GDP as well as for unit effects (assuming that the effects of GDP and inequality are constant across countries).21 The results are shown in Table 3.22 As expected, the effect of inequality is positive but insignificant. This holds regardless of the transformation of the dependent variable (models 1-4 vs. models 5-8), the inclusion of the LDV (columns 1, 2, 5, and 6) and the specification of a (common23 ) autoregressive term for the errors (models 2, 4, 6, and 8) . Given the data at hand, the conclusion is that there is no evidence for a negative effect of inequality on turnout.
2.2.4 Trivial Effect Size
Lister’s interpretation of his findings is driven almost exclusively by the statistical significance of the coefficients, and accordingly, much of the discussion in the two preceding sections has focused on the merits of various modelling techniques, the choice of estimators, and the statistical significance of parameter estimates. However, the findings from a statistical model should always be judged in terms of their substantive implications and political relevance (King et al., 2000).
After all, statistical significance is nothing but a statement about the conditional probability of observing an estimate of a given magnitude. In itself, such a probabilistic statement is not of substantive interest. First, it is easily possible that politically important effects go undetected because the respective significance test does not have enough power in small samples. Second, provided that the sample size is large, significance tests will pick up tiny deviations from the null hypothesis that are of no political consequence whatsoever. Therefore, statistical significance is entirely distinct from the substantive significance of the underlying factual claim. As a consequence, many significance tests that are routinely carried out are utterly insignificant in terms of their material implications (Gill, 1999).
The (disputed) statistically significance of inequality would simply imply that it is highly unlikely to come up with an estimate of this magnitude if the true value of this coefficient is exactly zero — not less, but certainly not more. It would not prove that inequality has any real-world consequence on turnout.
As it turns out, the analyses presented by Lister would not support his central argument — the institutions of the welfare state have an indirect impact on turnout — even if they were not conceptually and methodologically flawed and the estimates could be taken at face value. This is because the consequences of the alleged negative effect of inequality reported in Lister (2007) are negligible.
This fact is somewhat disguised by the non-linear transformation of the dependent variable but become readily apparent if one takes a closer look at Table 1 above. If all independent variables are at their mean, the expected transformed turnout is 1.613, that is 83.38 per cent (invlogit (1.613) × 100). If inequality is set to its empirical minimum of 27.08 (Sweden 1979), the expected turnout rate changes to 84.68 per cent (invlogit(1.710) × 100). If, on the other hand, inequality reaches its empirical maximum of 39.53 (Italy 1968), the expected turnout falls to invlogit(1.517) × 100 = 82.01 per cent — hardly a difference of any political relevance, even if it was significant in statistical terms.24
3 Conclusion
Michael Lister’s article makes a useful contribution to the (already very large) discussion on aggregate variables that foster or depress turnout by drawing attention to societal factors. But while the question of whether inequality reduces turnout in the aggregate is a relevant one, his analysis is fraught with methodological problems that call the validity of his findings into question. Firstly, the original article builds on an interesting theoretical argument about the impact of institutions on attitudes, from which a complex causal framework is derived, but Lister’s claims about causal relationship are not backed by data. Therefore, his analysis is confined to the question of whether there is a negative relationship between inequality and turnout in the aggregate. Secondly, no rationale is given for selecting this particular time-frame and sample of countries, and it is difficult to exactly reproduce the findings. Thirdly, Lister applies techniques developed by Beck and Katz to overcome the small-N problem of comparative politics. But since most of the control variables are constant within countries and highly correlated while the focal explanatory variable as well as the dependent variable are ‘sluggish’ (i.e. nearly constant within most countries), there are simply not enough truly independent observations to estimate the model specified by Lister.
By applying simple bootstrapping techniques it can be shown that the t-values reported by Lister are far too large, thereby overestimating the reliability/statistical significance of the parameters. This is confirmed by an alternative robustness test that applies Generalised Estimating Equations to the same data. Moreover, it can be demonstrated that the estimates change considerably if a single year, country or even a single observation is removed from the sample. Simple bivariate regression plots on a country-by-country basis as well as an alternative model that is less demanding than Lister’s specification confirm the assertion that there is no evidence for the supposed universal negative relationship between inequality and turnout.
Some of the problems outlined above can be traced back to Lister’s sole reliance on aggregate data. Over the past two decades, multi-level modelling techniques have been applied in subfields of political science as various as attitude formation (MacKuen and Brown, 1987), support for European integration (Gabel, 1998), recycling behaviour (Guerin et al., 2001) and the vote for the Extreme Right (Arzheimer and Carter, 2006), and the joint analysis of individual and macro-data would seem like an obvious remedy for at least some of the issues identified in the first part of this paper. As a case in point, in a recent contribution Anderson and Beramendi (2005) regress individual turnout on a number of individual and polity-level variables and find that income inequality at the macro-level reduces the probability of electoral participation.
But like PCSE, multi-level analysis is no panacea. Even if they are jointly analysed with individual-level information, data on the institutions of modern democracies will often be inherently ‘weak’ (Western and Jackman, 1994), because both the number of countries and the level of institutional variation within these countries is low, time-series are short, and strong unit effects are likely to prevail. This makes it extremely difficult to identify any causal effect.
Finally, it should be borne in mind that statistical significance is unrelated to substantive relevance. Even if the estimates and standard errors in Lister’s analysis could be taken at face value, they would not support the hypothesis that the institutions of the welfare state have an impact of turnout, because the political relevance of the alleged effects of inequality are negligible.
4 Figures and Tables
References
Anderson, C.J. and Beramendi, P. (2005) ‘Economic Inequality, Redistribution, and Political Inequality’, Paper prepared for presentation at the conference on ‘Income Inequality, Representation, and Democracy: Europe in Comparative Perspective.’, Maxwell School, Syracuse University, available at http://www.maxwell.syr.edu/moynihan/programs/euc/May6-7_Conference_Papers/Anderson%20and%20Beramendi%20EUC%20Conference%202005.pdf.
Anderson, D. and Davidson, P. (1943) The Democratic Class Struggle (Stanford: Stanford University Press).
Arellano, M. and Bond, S. (1991) ‘Some tests for specification for panel data: Monte carlo evidence and an application to employment equations’, Review of Economic Studies, 58, 277—297.
Arzheimer, K. and Carter, E. (2006) ‘Political opportunity structures and right-wing extremist party success’, European Journal of Political Research, 45, 419—443.
Atkinson, A.B. (2004) ‘The luxembourg income study (lis): Past, present and future’, Socio-Economic Review, 2, 165—190.
Atkinson, A.B. and Brandolini, A. (2000) ‘Promise and pitfalls in the use of ’secondary’ data-sets: Income inequality in OECD countries’, Temi di discussione (Economic working papers) 379, Bank of Italy, Economic Research Department, available at http://ideas.repec.org/p/bdi/wptemi/td_379_00.html.
Beck, N. (2001) ‘Time-series-cross-section data. what have we learned in the past few years?’, Annual Review of Political Science, 4, 271—293.
Beck, N. (2007) ‘From statistical nuisances to serious modeling: Changing how we think about the analysis of time-series-cross-section data’, Political Analysis, 15, 97—100.
Beck, N. and Katz, J.N. (1995) ‘What to do (and not to do) with time-series cross-section data’, American Political Science Review, 89, 634—647.
Beck, N. and Katz, J.N. (1996) ‘Nuisance vs. substance: Specifying and estimating time-series-cross-section models’, Political Analysis, 6, 1—36.
Berk, R.A. (2004) Regression Analysis. A Constructive Critique (Thousand Oaks, London, New Delhi: Sage).
Berk, R.A., Western, B. and Weiss, R.E. (1995) ‘Statistical inference for apparent populations’, Sociological Methodology, 25, 421—458.
Coleman, J.S. (1994) Foundations of Social Theory (Cambridge, London: The Belknap Press of Harvard University Press).
Efron, B. and Tibshirani, R.J. (1993) An Introduction to the Bootstrap (New York: Chapman and Hall).
Fisher, S.D. (2007) ‘(change in) turnout and (change in) the left share of the vote’, Electoral Studies, 26:3, 598—611.
Gabel, M. (1998) ‘Public support for european integration. an empirical test of five theories’, Journal of Politics, 60, 333—354.
Gallagher, M. (1991) ‘Proportionality, disproportionality and electoral systems’, Electoral Studies, 10, 33—51.
Geys, B. (2006) ‘Explaining voter turnout. a review of aggregate-level research’, Electoral Studies, 25, 637—663.
Gill, J. (1999) ‘The insignificance of null hypothesis significance testing’, Political Research Quarterly, 52, 647—674.
Gratschew, M. (2001) Compulsory Voting (http://www.idea.int/vt/compulsory_voting.cfm (04.06.2007): IDEA).
Guerin, D., Crete, J. and Mercier, J. (2001) ‘A multilevel analysis of the determinants of recycling behavior in the european countries’, Social Science Research, 195—218.
Huber, E., Ragin, C., Stephens, J.D., Brady, D. and Beckfield, J. (2004) Comparative Welfare States Data Set (http://www.lisproject.org/publications/welfaredata/welfareaccess.htm (04.06.2007): Northwestern University, University of North Carolina, Duke University and Indiana University).
King, G. (1997) A Solution to the Ecological Inference Problem. Reconstructing Individual Behavior from Aggregate Data (Princeton: Princeton University Press).
King, G., Tomz, M. and Wittenberg, J. (2000) ‘Making the most of statistical analysis. improving interpretation and presentation’, American Journal of Political Science, 44, 341—355.
Lijphart, A. (1984) Democracies. Patterns of Majoritarian and Consensus Government in Twenty-one Countries (Stanford: Stanford University Press).
Lijphart, A. (1999) Patterns of Democracy. Government Forms and Performance in Thirty-Six Countries (New Haven: Yale University Press).
Lister, M. (2007) ‘Institutions, inequality and social norms: Explaining variations in participation’, British Journal of Politics and International Relations, 9, 20—35.
Mackie, T.T. and Rose, R. (1982) The International Almanac of Electoral History (Houndmills, London: Macmillan).
MacKuen, M. and Brown, C. (1987) ‘Political context and attitude change’, The American Political Science Review, 81:2, 471—490.
Ostrom, C.W. (1990) Time Series Analysis. Regression Techniques (Newbury Park, London, New Delhi: Sage).
Plümper, T. and Troeger, V.E. (2007) ‘Efficient estimation of time-invariant and rarely changing variables in finite sample panel analyses with unit fixed effects’, Political Analysis, 15:2, 124—139.
Powell Bingham, G. (1986) ‘American voter turnout in comparative perspective’, The American Political Science Review, 80, 17—43.
Robinson, W.S. (1950) ‘Ecological correlation and the behavior of individuals’, American Sociological Review, 15, 351—357.
Shor, B., Bafumi, J., Keele, L. and Park, D. (2007) ‘A bayesian multilevel modeling approach to time-series cross-sectional data’, Political Analysis, 15:2, 165—181.
University of Texas Inequality Project (2004) Estimated Household Income Inequality Data Se (http://utip.gov.utexas.edu/data/UTIP_UNIDO2001rv3.xls (04.06.2007): University of Texas).
Western, B. and Jackman, S. (1994) ‘Bayesian inference for comparative research’, American Political Science Review, 88, 412—423.
Wilson, S.E. and Butler, D.M. (2007) ‘A lot more to do: The sensitivity of time-series cross-section analyses to simple alternative specifications’, Political Analysis, 15:2, 101—123.
Zorn, C.J.W. (2001) ‘Generalized estimating equation models for correlated data: A review with applications’, American Journal of Political Science, 45:2, 470—490.
*Thanks to Sarah Kirschmann for research assistance and Elisabeth Carter, Harald Schoen, and two anonymous reviewers for their valuable comments and suggestions. Needless to say, the usual disclaimer applies.
1One could even argue that causality works the other way around: a constantly high level of turnout (which is indicative of a mobilised working class) forces the government to maintain a high level of welfare state protection.
2Information on federalism, bicameralism and presidentialism is drawn from Lijphart (1984, 1999), although there is an inconsistency in the data set: Lijphart (1999, 189) codes federalism with integers ranging from ‘1’ (unitary states with no elements of de-centralisation) to ‘5’ (strong federal arrangements). In Huber et al. (2004), this scale reduced to just three integers (0-2= no/weak/strong federalism) in a not entirely transparent way. Particularly confusing is the case of Belgium, which is coded as ‘0’ until 1993 although it is assigned a value of ‘3’ by Lijphart (1999).
3Moreover, the measure for the proportionality of the electoral system (SINGMEMD) (which is apparently not drawn from Powell’s (1986) seminal paper but rather from Lijphart (1984, 1999)) is a static index, while there is now ample evidence that proportionality is best understood as the result of the dynamic interaction between electoral rules on the one hand and the fragmentation and spatial distribution of party support on the other hand (see e.g. Gallagher 1991. At any rate, it is unlikely that an index will have a linear effect. Like federalism and bicameralism, it should probably be replaced by a series of dummy variables.
4First, including a lagged dependent variable (turnout at point t -1) would normally imply that the first wave of the panel is lost, but here it is possible to retain the first wave since turnout was recorded for the elections preceding the cut-off year of 1963. Second, the data on compulsory voting (Gratschew, 2001) are somewhat ambiguous with regard to Austria, the Netherlands, and Italy. Finally, the UK (1974) and Ireland (1982) held two general elections in a single year, and various solutions for dealing with this problem are conceivable.
5Calculated for those 129 election years for which complete information is available and treating Australia, Belgium, and Italy as having compulsory voting.
6Apparently, no such transformation was applied to the lagged dependent variable.
7In practice, the predicted values are well-behaved even without the transformation, and predictions based on the original and the transformed values are extremely highly correlated (r = 0.99). Whatever the transformation’s utility, while a discussion of the procedure and the rationale for its application could be relegated to an appendix, the fact that the variable was transformed should be mentioned in the article.
8Bingham Powell’s index refers to French presidential elections and classifies them as very proportional, which seems rather odd. Nonetheless, the coding scheme discussed by Lister (2007, 30) suggests that this variable was used in the original analysis. My replication data set also includes the alternative variable provided by Huber et al. (2004), but the substantive conclusions are the same, regardless of which operationalisation is chosen.
9Non-spherical errors also render the parameter estimates inefficient, but this is usually considered a minor problem (Beck and Katz, 1995, 636).
10While there are historical events like the oil price crises that might affect turnout in all countries in a given year, it is not easy to conceive of an error process that affects say the second election in the period of study in each or even most countries in the same way. Yet, such effects are not entirely implausible. For instance, in five countries, the second election under study was held in the eventful year of 1968.
11Another panel estimator with desirable properties was proposed by Arellano and Bond (1991). However, the Arellano-Bond estimator involves first differences of the independent variables and can therefore not deal with those regressors that are (almost) constant within panels. An Arellano-Bond regression of turnout on the dynamic variables (GDP and inequality) is therefore not fully comparable to the results in Table 2 but demonstrates again that inequality has no significant effect (not shown as a table).
12In Sweden, STRBIC changes from ‘weak bicameralism’ to ‘no second chamber or second chamber with very weak powers’ after a constitutional reform in 1970.
13A wider definition of unit effects would include country-specific slopes and error variances, see Wilson and Butler 2007, 104.
14See the figures in Wilson and Butler for graphical examples. The inclusion of the LDV in the model does not necessarily capture unit effects (Wilson and Butler, 2007, 107).
15Goodman and Kruskal’s γ = 0.53.
16γ = -0.64.
17West Germany is another high-turnout country. The rather low value in 1990 is actually a combined figure for both West and East Germany.
18The inclusion of the LDV also changes the interpretation of the coefficients for the independent variables because the impact of x will cumulate over time (Ostrom, 1990, 72-74). The situation is even more complicated here because the lagged endogenous variable was apparently not transformed. See footnote 24 for an explanation.
19A more general and almost philosophical question is whether ‘apparent populations’ should be treated as samples at all. See the exchange initiated by Berk et al. (1995) and the monograph by Berk (2004, 42-56) for a critical assessment.
20To ease interpretation, actual turnout was plotted against inequality. Analyses using the transformed variable (LOGITVTURN) lead to essentially the same conclusions.
21See Plümper and Troeger (2007) for an interesting new approach that aims at giving biased but relatively efficient estimates for the effects of slowly changing or time-invariant variables in the presence of unit-effects.
22The four French elections and the German election of 1990 were removed from the sample for reasons stated above.
23As explained above, it seems unwise to estimate panel-specific autoregressive terms.
24The issue is actually slightly more complicated because (a) Lister’s specification includes a LDV, which implies that the present effect indirectly affects future levels of turnout and (b) because the dependent is transformed in a non-linear fashion while the LDV is retained in its original scale, thereby creating a complex linear-non-linear feedback loop. As a consequence, turnout would rapidly (within 10 elections) converge towards 100 per cent if the process starts from the mean values in Table 1 and is otherwise left alone. However, this convergence depends on the initial level of turnout. Setting inequality to its maximum and thereby reducing the initial level of turnout to 82 per cent is sufficient to trigger a convergence towards a 0 per cent turnout rate, again within the course of ten elections. The decision over whether such a specification make sense substantially is left to the reader.
Discover more from kai arzheimer
Subscribe to get the latest posts sent to your email.

